مقدمه ای ملایم بر آمار بیزی

تصویر از Pexels (عکس از Balazs Utasi)

آمار بیزی یکی از غیر متعارف ترین زیرشاخه های آمار است که بر اساس دیدگاه خاصی از مفهوم احتمال است. این مقاله از طریق روایتی ملایم و اساساً غیر فنی که کنجکاوی شما را در مورد این موضوع جذاب برانگیخته می‌کند و نشان می‌دهد که آمار بیزی چیست و تفاوت‌های آن با آمارهای مکررگرا چیست.

مقدمه

آمار مجموعه ای ارزشمند از روش ها و ابزارها برای تجزیه و تحلیل و اتخاذ تصمیمات مبتنی بر داده است. کاربرد آنها در زمینه های مختلف برای دهه ها و حتی قرن ها از زمان تولد آمار به عنوان یک رشته در قرن هجدهم وجود داشته است.

به طور سنتی، آمار با اتخاذ الف مورد مطالعه و اعمال قرار گرفته است رویکرد مکررگرابر اساس این ایده که احتمال یک رویداد با بسامد وقوع آن رویداد پس از تعداد زیادی آزمایش یا آزمایش توصیف می شود.

با این حال، یک رویکرد آماری کمتر شناخته شده اما به همان اندازه قدرتمند وجود دارد: رویکرد بیزیبیایید دریابیم که این رویکرد چیست.

آمار بیزی ابهام زدایی کرد

آمار بیزی امکان ادغام اطلاعات قبلی را که اغلب ماهیت ذهنی دارند در تجزیه و تحلیل آماری ممکن می سازد. این می تواند منجر به نتیجه گیری یا تصمیماتی شود که در موارد خاص با واقعیت سازگارتر باشد.

این ویژگی آمار بیزی آنها را با یک ایده مرکزی از آمارهای متداول متمایز می کند: تفسیر احتمالات. برخلاف آمارهای فراوان گرا، که در آن احتمال به عنوان فراوانی درازمدت یک رویداد درک می شود، که نیازمند تعداد معینی آزمایش و مشاهدات قبلی است، در آمار بیزی، احتمال به عنوان درجه ای از باور یا قطعیت درک می شود. اگر شواهد یا اطلاعات جدیدی در مورد پدیده مورد مطالعه در دسترس باشد، ممکن است این معیار به روز شود. به این ترتیب، روش‌های بیزی می‌توانند دانش یا فرضیه‌های قبلی را ترکیب کنند، در حالی که آمارهای متداول منحصراً بر داده‌های جمع‌آوری‌شده در طول آزمایش مورد مطالعه تمرکز می‌کنند.

آنچه در ادامه می آید مثال تفاوت های اساسی بین آمار متداول و بیزی را نشان می دهد:

فرض کنید یک پزشک می خواهد احتمال P(H|E) را محاسبه کند که یک بیمار پس از کسب نتیجه مثبت در یک آزمایش تشخیصی در مرحله آزمایشی، از یک بیماری نادر رنج می برد. در اینجا، P(H|E) احتمال خلفی است، جایی که H رویدادی است که بیمار به بیماری مبتلا شده است و E شواهدی است، مانند نتیجه آزمایش تشخیصی مثبت.

• از یک دیدگاه مکررگراپزشک برای محاسبه احتمال P(H|E) میزان مثبت کاذب (بیماران مثبت و فاقد بیماری) و میزان شیوع بیماری در جمعیت بزرگتر را در نظر می گیرد. هیچ سابقه یا اطلاعاتی از بیمار در این محاسبه احتمال ابتلا به بیماری پس از مثبت شدن آزمایش استفاده نمی شود.
• در همین حال، الف دیدگاه بیزی پزشک می‌تواند اطلاعات قبلی در مورد بیمار، مانند علائم گذشته و حال و سابقه پزشکی را در محاسبه احتمال لحاظ کند. اگر علائم ارائه شده مربوط به بیماری باشد، پزشک می تواند احتمال اولیه ابتلای بیمار به آن را تنظیم کند و آن را بر اساس نتیجه آزمایش تشخیصی به روز کند.

به طور خلاصه، یک رویکرد بیزی دید شخصی‌تر از احتمالات را ارائه می‌کند، بنابراین وضعیت واقعی بیمار را به طور صادقانه‌تری منعکس می‌کند.

به طور رسمی، رشته آمار بیزی بر چندین مفهوم، روش و تکنیک استوار است. چهار رکن اساسی که برای کسانی که می خواهند با این شاخه از آمار آشنا شوند، مفاهیم اساسی را تشکیل می دهند، عبارتند از:

1. قضیه بیز: این فرمول مرکزی است که بر اساس آن روش های رسمی برای محاسبه احتمالات به روز و دقیق بر اساس شواهد جدید ارائه شده است.
2. احتمال پیشینی و پسینی: احتمال پیشینی P(H) باور اولیه در مورد احتمال یک رویداد H قبل از ترکیب یک عنصر شواهد (E) است، در حالی که احتمال P(H|E) این رویداد پس از مشاهده اثبات به عنوان احتمال پسین شناخته می شود. .
3. استنتاج بیزی: مجموعه ای از روش ها و فرآیندهایی که از طریق آنها از قضیه بیز برای به روز رسانی احتمالات مبتنی بر باور استفاده می شود.
4. نمونه گیری زنجیره مارکوف مونت کارلو (MCMC): روش تقریب توزیع احتمالات پسین با رسم نمونه به صورت تصادفی

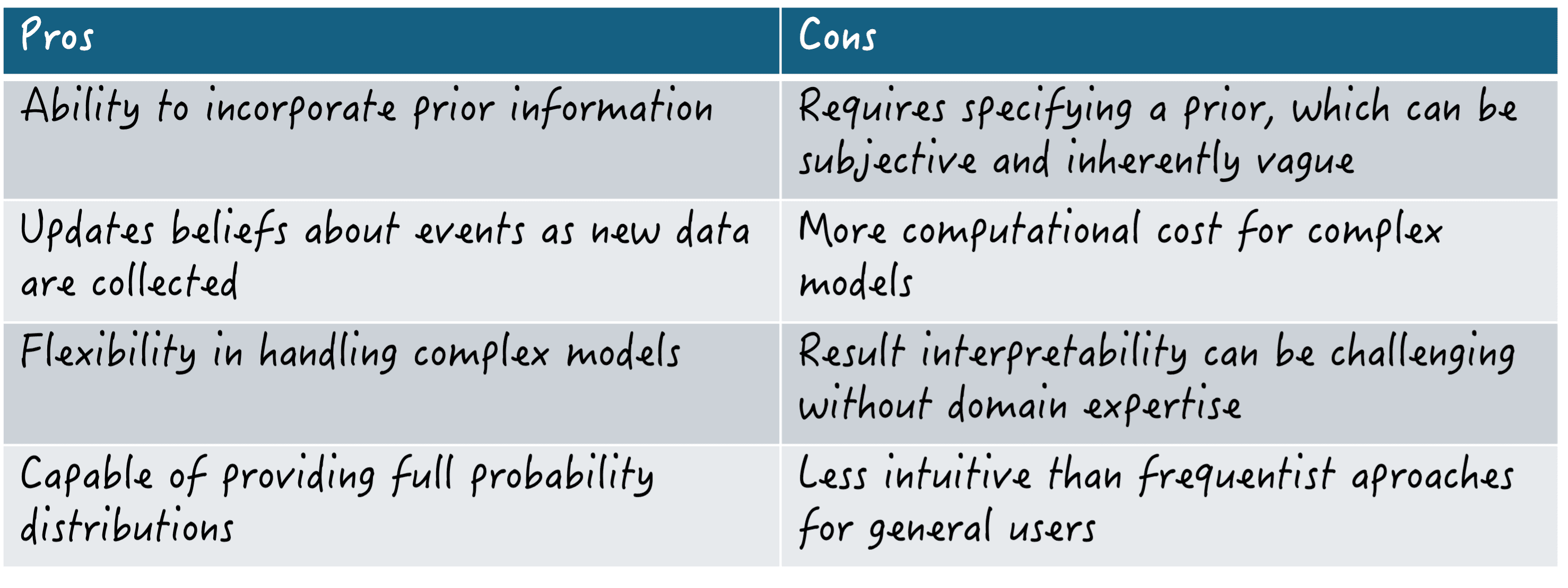
مزایا و معایب آمار بیزی

جدول زیر برخی از مزایا و معایب روش‌ها و روش‌های آماری بیزی را در مقایسه با روش‌های متداول سنتی، خلاصه می‌کند.

کاربردهای آمار بیزی

ما با فهرست کردن برخی از حوزه‌های کاربردی که در آن‌ها آمار بیزی با موفقیت در عمل اعمال شده‌اند، پایان می‌دهیم.

• یادگیری ماشین و هوش مصنوعی، به ویژه در مدل‌های احتمالی و الگوریتم‌های یادگیری تقویتی که به شدت بر تکنیک‌های آماری بیزی متکی هستند.
• مدل سازی مالی برای ارزیابی ریسک و فرآیندهای پیش بینی
• مراقبت های بهداشتی و تشخیص پزشکی، برای پیش بینی بیماری و ارزیابی خطر بیمار
• علوم زیست محیطی، برای مدل سازی الگوهای آب و هوا و ارزیابی خطرات برای تنوع زیستی و اکوسیستم ها
• تجزیه و تحلیل بازاریابی و رفتار مصرف کننده در خرده فروشی و همچنین پیش بینی تقاضای محصول

نتیجه گیری

این مقاله مروری ساده و غیر فنی از آمار بیزی ارائه می‌کند و تفاوت‌های اصلی آن را با رویکردهای آماری کلاسیک برجسته می‌کند و برخی از حوزه‌های کاربردی آن را توصیف می‌کند. برای کسانی که مایل به تعمیق دانش خود هستند، ما شما را تشویق می کنیم که به کاوش در پیچیدگی های این مجموعه قدرتمند و همه کاره از روش های آماری بر اساس مفاهیم و مفاهیم کلیدی ذکر شده در بالا ادامه دهید.