10 تک لاینر پایتون برای ایجاد ویژگی های سری زمانی

جدول محتوا

مقدمه

داده های سری زمانی معمولاً برای ساختن مدل‌های پیش‌بینی مؤثر و روشنگر به درک عمیق نیاز دارد. دو ویژگی کلیدی برای پیش‌بینی سری‌های زمانی ضروری است: نمایندگی و دانه بندی.

بازنمایی شامل استفاده از رویکردهای معنادار برای تبدیل داده های زمانی خام – برای مثال اندازه گیری روزانه یا ساعتی – به مدل های آموزنده است.
دانه بندی در مورد تجزیه و تحلیل دقیق این مدل ها تغییرات در طول زمان است.

به عنوان دو روی یک سکه، تفاوت آنها ظریف است، اما یک چیز مسلم است: هر دو از طریق به دست می آیند. مهندسی ویژگی.

این مقاله 10 خط ساده پایتون را برای تولید ویژگی‌های سری زمانی بر اساس ویژگی‌ها و ویژگی‌های مختلف زیربنای داده‌های سری زمانی خام ارائه می‌کند. این خطوط تک خطی را می توان به صورت مجزا یا ترکیبی استفاده کرد تا به شما کمک کند مجموعه داده های آموزنده تری ایجاد کنید که چیزهای زیادی را در مورد رفتار زمانی داده های شما نشان می دهد: چگونه تغییر می کند، چگونه نوسان می کند و چه روندهایی را در طول زمان نشان می دهد.

توجه داشته باشید که نمونه های ما استفاده می کنند پانداها و NumPy.

1. تابع Shift (نمایش خود رگرسیون)

ایده پشت استفاده از نمایش های خودبازگشتی یا ویژگی های تاخیر ساده تر از آن چیزی است که به نظر می رسد: این است که مشاهده قبلی را به عنوان یک ویژگی پیش بینی کننده جدید در مشاهده فعلی اضافه کنیم. در اصل، این احتمالاً ساده‌ترین روش برای نمایش وابستگی زمانی است، برای مثال بین لحظه فعلی و لحظه‌های قبلی.

به عنوان اولین نمونه کد تک خطی در این لیست 10 تای، اجازه دهید نگاهی دقیق تر به این یکی بیندازیم.

این مثال تک خطی فرض می کند که شما مجموعه ای از داده های سری زمانی خام را در a ذخیره کرده اید DataFrame تماس گرفت dfیکی از صفات موجود نام دارد 'value'. توجه داشته باشید که استدلال در shift() عملکرد را می توان برای بازیابی مقدار ذخیره شده تنظیم کرد n لحظاتی از زمان یا مشاهدات قبل از لحظه فعلی:

df[‘lag_1’] =df[‘value’].shift(1)

df[‘lag_1’] = df[‘value’].تغییر دهید(1)

برای داده‌های سری زمانی روزانه، اگر می‌خواهید مقادیر قبلی را برای یک روز معین از هفته، مثلا دوشنبه، ثبت کنید، منطقی است که از آن استفاده کنید. shift(7).

2. میانگین متحرک (هموارسازی کوتاه مدت)

برای ثبت روندهای محلی یا نوسانات کوتاه مدت در داده ها، معمولاً استفاده از روش های چرخشی در سراسر کشور عملی است. n مشاهدات گذشته منتهی به مشاهدات کنونی: این یک راه ساده اما بسیار مفید برای هموارسازی مقادیر سری زمانی خام و گاه بی نظم در یک ویژگی معین است.

این مثال یک مشخصه جدید ایجاد می کند که برای هر مشاهده، میانگین چرخشی سه مقدار قبلی این مشخصه در مشاهدات اخیر را شامل می شود:

df[‘rolling_mean_3’] =df[‘value’].rolling(3).mean()

df[‘rolling_mean_3’] = df[‘value’].بلبرینگ(3).معنی()

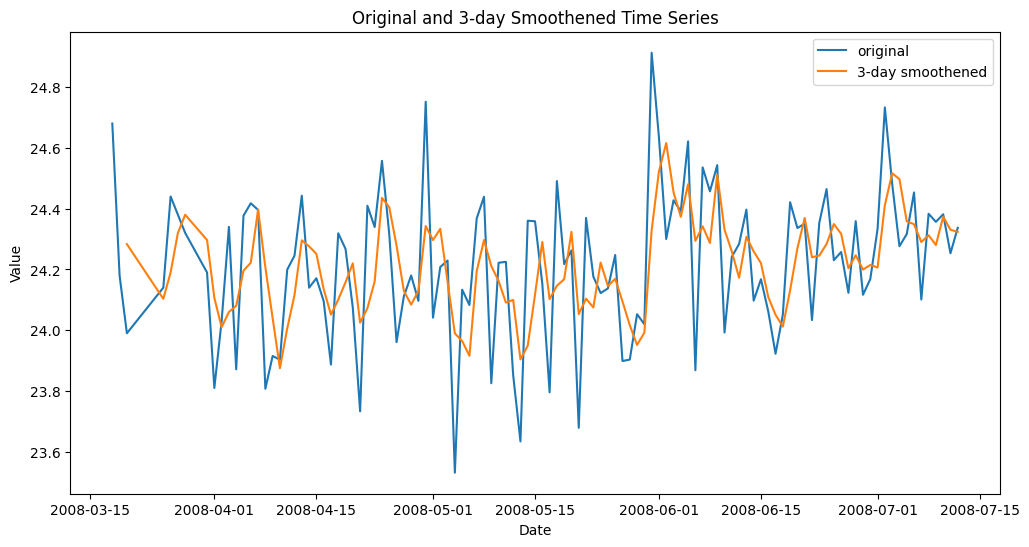
عملکرد سری زمانی هموار با میانگین متحرک

3. انحراف استاندارد چرخشی (نوسانات محلی)

مشابه میانگین‌های نورد، قابلیت ایجاد ویژگی‌های جدید بر اساس انحراف استاندارد نورد نیز وجود دارد که برای مدل‌سازی نوسانات مشاهدات متوالی مؤثر است.

این مثال عملکردی را برای مدل‌سازی تغییرپذیری آخرین مقادیر در یک پنجره متحرک یک هفته‌ای با فرض مشاهدات روزانه معرفی می‌کند.

df[‘rolling_std_7’] =df[‘value’].rolling(7).std()

df[‘rolling_std_7’] = df[‘value’].بلبرینگ(7).استاندارد()

4. گسترش میانگین (حافظه تجمعی)

گسترش میانگین‌گیری، میانگین تمام نقاط داده را تا (و شامل) مشاهده فعلی در توالی زمانی محاسبه می‌کند. بنابراین یک میانگین متحرک با اندازه پنجره به طور مداوم در حال افزایش است. تجزیه و تحلیل این که چگونه میانگین مقادیر یک ویژگی سری زمانی در طول زمان تغییر می کند، مفید است، در نتیجه روندهای صعودی یا نزولی با اطمینان بیشتری در دراز مدت ثبت می شود.

df[‘expanding_mean’] =df[‘value’].expanding().mean()

df[‘expanding_mean’] = df[‘value’].گسترش().معنی()

5. تفاوت (حذف روند)

این تکنیک برای حذف روندهای بلندمدت، برجسته کردن نرخ‌های تغییر – که در سری‌های زمانی غیر ثابت برای تثبیت آنها مهم است، استفاده می‌شود. تفاوت بین مشاهدات متوالی (جاری و قبلی) یک ویژگی هدف را محاسبه می کند:

df[‘diff_1’] =df[‘value’].diff()

df[‘diff_1’] = df[‘value’].تفاوت()

6. ویژگی های مبتنی بر زمان (استخراج مولفه های زمانی)

ساده اما بسیار مفید در برنامه های کاربردی دنیای واقعی، این تک خط می تواند برای تجزیه و استخراج اطلاعات مربوطه از تابع تاریخ کامل یا فهرست بندی سری های زمانی شما در اطراف استفاده شود:

df[‘month’]df[‘dayofweek’] =df[‘Date’].dt.month، df[‘Date’].dt.dayoftheweek

df[‘month’]، df[‘dayofweek’] = df[‘Date’].dt.ماه، df[‘Date’].dt.روز هفته

مهم: مراقب باشید و بررسی کنید که آیا در سری زمانی خود اطلاعات تاریخ-زمان در یک ویژگی معمولی یا به عنوان شاخصی از ساختار داده وجود دارد. اگر این شاخص بود، ممکن است لازم باشد از این استفاده کنید:

df[‘hour’]df[‘dayofweek’] = df.index.hour، df.index.dayofweek

df[‘hour’]، df[‘dayofweek’] = df.اشاره.ساعت، df.اشاره.روز هفته

7. همبستگی لغزشی (رابطه زمانی)

این رویکرد فراتر از آمارهای چرخشی در یک پنجره زمانی است تا میزان همبستگی مقادیر اخیر را با همتایان عقب افتاده خود اندازه گیری کند و به کشف همبستگی خودکار در حال تکامل کمک کند. این برای مثال برای تشخیص تغییرات رژیم مفید است، یعنی تغییرات رفتاری ناگهانی و مداوم در داده‌ها در طول زمان، که زمانی رخ می‌دهد که همبستگی‌های چرخشی شروع به ضعیف شدن یا معکوس شدن در یک نقطه زمانی معین می‌کنند.

df[‘rolling_corr’] =df[‘value’].rolling(30).corr(df[‘value’].shift(1))

df[‘rolling_corr’] = df[‘value’].بلبرینگ(30).تصحیح(df[‘value’].تغییر دهید(1))

8. ویژگی های فوریه (فصلی)

تبدیل فوریه سینوسی را می توان در ویژگی های خام سری های زمانی برای ثبت الگوهای چرخه ای یا فصلی استفاده کرد. به عنوان مثال، اعمال تابع سینوس (یا کسینوس) اطلاعات چرخه‌ای روز از سال را که در زیر ویژگی‌های تاریخ-زمان قرار دارند، به ویژگی‌های پیوسته و مفید برای یادگیری و مدل‌سازی الگوهای سالانه تبدیل می‌کند.

df[‘fourier_sin’] = np.sin(2 * np.pi * df[‘Date’].dt.dayofyear / 365) df[‘fourier_cos’] = np.cos(2 * np.pi * df[‘Date’].dt.dayoftheyear / 365)

df[‘fourier_sin’] = n.p..ماهیگیری(2 * n.p..پی* df[‘Date’].dt.روز سال / 365)

df[‘fourier_cos’] = n.p..چون(2 * n.p..پی * df[‘Date’].dt.روز سال / 365)

اجازه دهید در این مثال به جای تک خط از یک دو خطی استفاده کنم، به یک دلیل: سینوس و کسینوس با هم در به تصویر کشیدن یک نمای کلی از الگوهای فصلی چرخه ای احتمالی بهتر هستند.

9. میانگین وزنی نمایی (هموارسازی تطبیقی)

میانگین وزنی نمایی – یا به اختصار EWM – برای به دست آوردن وزن های در حال فروپاشی نمایی استفاده می شود که در عین حفظ حافظه بلندمدت، اهمیت بیشتری به مشاهدات داده های اخیر می دهد. این یک رویکرد تطبیقی تر و تا حدودی “هوشمندانه” است که مشاهدات اخیر را نسبت به گذشته های دور اولویت قرار می دهد.

df[‘ewm_mean’] =df[‘value’].ewm(span=5).mean()

df[‘ewm_mean’] = df[‘value’].اوم(دامنه=5).معنی()

10. آنتروپی نورد (پیچیدگی اطلاعات)

کمی ریاضی بیشتر برای آخرین! آنتروپی لغزشی یک ویژگی معین در یک پنجره زمانی، میزان تصادفی شدن یا پراکندگی مقادیر در آن پنجره زمانی را محاسبه می‌کند، در نتیجه میزان و پیچیدگی اطلاعات موجود در آن را آشکار می‌کند. مقادیر پایین تر آنتروپی غلتشی حاصل، حس نظم و قابلیت پیش بینی را نشان می دهد، در حالی که هر چه این مقادیر بالاتر باشد، “آشوب و عدم اطمینان” بیشتر است.

df[‘rolling_entropy’] =df[‘value’].rolling(10).apply(lambda x: -np.sum((p:=np.histogram(x, bins=5)[0]/len(x))*np.log(p+1e-9)))

df[‘rolling_entropy’] = df[‘value’].بلبرینگ(10).اعمال شود(لامبدا x: –n.p..مجموع((ص:=n.p..هیستوگرام(x، سطل زباله=5)[0]/لن(x))*n.p..ذخیره کنید(ص+1–9)))

نتیجه گیری

در این مقاله، ما 10 استراتژی – که هر کدام یک خط کد را پوشش می‌دهند – برای استخراج انواع الگوها و بینش‌ها از داده‌های سری زمانی خام، از ساده‌ترین روندها گرفته تا موارد پیچیده‌تر مانند فصلی بودن و پیچیدگی اطلاعات، بررسی و نشان دادیم.

منبع:aitoolsclub.com/